Una proporción es la relación entre dos razones, una comparación entre dos razones.
Euclides estableció la proporción áurea mediante la división de un segmento por un punto dado de manera que la línea o segmento entero respecto al segmento medio de la división es igual a la relación entre el segmento medio y el menor de la división. El cociente entre cada par de razones es de forma aproximada 1,61803, también llamado nº de oro. Se puede expresar también mediante uno más raíz de cinco partido dos. Si al segmento medio lo llamamos x y al menor uno, como tenemos que la línea se separa en extrema y media razón, x es a 1 como 1 + x es a x.
X/1=(x + 1)/x
Despejando tenemos que x al cuadrado menos x menos 1 es igual a 0,
esta ecuación de segundo grado se resuelve de la siguiente forma: x igual a menos b más menos, raíz cuadrada de b al cuadrado menos 4 por a y por c partido todo por dos por a; siendo a, b, c los tres términos de la ecuación, 1º, 2º y 3º respectivamente.
Cuando phi es positivo el valor es 1,6180339887, también llamado nº de oro.
A continuación mostramos algunos decimales correspondientes al número de oro
(valor del cociente entre dos segmentos de la proporción): 1,61803 39887 49894 84820 45868 34365 63811 77203 09179 80576 28621 35448 62270 52604 62818 90244 97072 07204 18939 11374 Si elevamos al cuadrado el número de oro tenemos el mismo número más la unidad: 1,61803 al cuadrado = 2,61803 Si dividimos uno entre el número de oro , obtenemos 0,618 que es la otra solución a la ecuación de segundo grado, sin tener en cuenta el negativo de la misma:
1/1,61803= 0,61803
La proporción áurea no se puede expresar como un número racional, no se puede obtener un número
común que este contenido equis veces en el segmento medio y otro número de veces
en el segmento menor, por esto se llaman longitudes inconmensurables, y son aquellas
Existe una relación de proporción en la que se cumple que un segmento mayor a+b
es al medio a como el medio a es al menor b, al tiempo que la suma del segmento medio a y menor b es igual al segmento mayor (a +b), a esta relación de proporción se le llama áurea.
En el dibujo podemos verificar que esto es cierto, se trata de demostrar que el segmento
mayor (a +b), es al medio a como éste al menor b y la suma del medio a y el menor b es igual al mayor (a +b). Para ello proyectamos el segmento mayor (a +b) sobre otro segmento “medio” c (que es igual a a), al proyectar mediante una recta paralela el segmento medio a sobre el mismo segmento obtenemos otro segmento d que es igual al menor d, de esta forma observamos que el segmento mayor es al medio como el medio es al menor y al tiempo la suma del medio y menor es igual al mayor.
Para mayor claridad se ha concretado de forma numérica dando al segmento medio el
valor uno. De esta forma al dividir el segmento mayor entre uno sabemos que va a dar el valor del número áureo, con lo que estamos obligados a considerar el segmento mayor con el valor de 1,618. La diferencia de ambos provoca que el segmento menor sea 0,618. El mayor entre el medio tiene como cociente 1,618 y análogamente el medio entre el menor tiene el mismo valor.
Si cambiamos los términos de la proporción tenemos que (a+b)/a=a/b se transforma en
b/a=a/(a+b), tenemos por tanto que 0,618 es a uno, como uno es 1,618. En este caso el cociente entre ambos términos es 0,618, el otro valor de la ecuación de segundo grado que no se utiliza por tener signo negativo. 
Podemos comprobar que la relación que establece la proporción áurea para 2
segmentos cualesquiera a b, por regla general no se cumple. En la figura tenemos un segmento dividido en dos partes, un segmento medio b y otro menor c , la suma de ambos es igual al segmento mayor a, tenemos: (a= b+c). Gráficamente proyectamos el segmento mayor a y lo transformamos en el segmento medio b=b’, al proyectar en la misma dirección el segmento medio b observamos que se transforma en otro segmento distinto de c, diferente del menor, como exigiría la proporción áurea, con lo cual tenemos que no se verifica que el mayor es al medio como el medio es al menor. 
Podemos coger un segmento, por ejemplo 13,6, y multiplicarlo por 1,618, de esta forma
tenemos el segmento menor y el segmento medio. A continuación podemos por el teorema de Thales transformarlos de manera que la suma de ambos se transformen en el segmento medio y el segmento medio se transforme en el menor. Pero este detalle no nos dicen nada de cómo poder construir el número de oro, ya que partimos de su conocimiento.  Para obtenerlo podemos seguir el siguiente procedimiento:
Tenemos un segmento AB y debemos obtener otro BC que esté en proporción
áurea con él. Construimos un cuadrado ABCD a partir del segmento base AB y haciendo centro en su punto medio O hacemos una circunferencia que pase por los otros dos vértices del cuadrado FD. Esta circunferencia corta a la prolongación de la base del cuadrado AB en un punto C, este punto es el del segmento BC que está en proporción áurea con el segmento dado AB. Podemos comprobar que ello es cierto aplicando el teorema de Tales pues al transformar el segmento mayor AC en el segmento medio FA del lado vertical del cuadrado igual a AB y al hacer por el punto B una paralela BH a esta dirección FC obtenemos el segmento menor HA y comprobamos que tiene la dimensión BC al trasladar mediante un giro de centro O este segmento menor BC a su nueva posición GA y al hacer centro en A la nueva circunferencia de radio GA observamos que es coincidente con el radio HA. Queda demostrado por tanto en el dibujo que el segmento mayor AC es al medio AB o FA como el medio es al menor BC o AH, siendo él mismo tiempo el segmento mayor AC igual a la suma de los otros dos AB, BC. -------------------------------- 
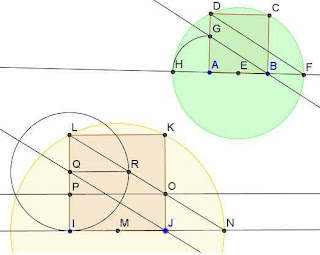
En la figura inferior podemos observar un cuadrado amarillo de lado b.
Haciendo centro en el punto medio del lado y tomando como radio la distancia de ese punto a cualquiera de los vértices superiores, por ejemplo el punto H, hacemos un arco hasta que corta a la prolongación del lado en un punto M. Desde la conclusión del lado b a ese punto M tenemos un nuevo segmento c. El lado del cuadrado b y este nuevo segmento c están en proporción áurea. Como podemos observar los dos segmentos en proporción áurea bc suman el segmento a.
Para demostrar gráficamente que esta relación es válida, proyectamos a la parte
superior del segmento total a y colocamos a su derecha y en el extremo el cuadrado amarillo de lado b. Proyectamos también el segmento c sobre la prolongación del segmento a. Haciendo centro en el punto medio del segmento a+c construimos una semicircunferencia que corta al cuadrado en el extremo superior.
Se tiene por tanto que el lado del cuadrado b es media proporcional entre el segmento
a que es la suma de los dos b+c y el segmento c, queda en consecuencia demostrado gráficamente la relación que existe entre los tres segmentos, a saber: a es igual a b más c, el segmento a es al segmento b como el segmento b es al segmento c. --------------------------------
Si cogemos dos números cualesquiera (3 y 8, p. ej.) y los sumamos obtenemos un nuevo
número 11 que lo sumamos al anterior 8 y así de forma sucesiva , después de operar con unos cuantos dividimos dos números consecutivos , el mayor entre el menor y observamos que el cociente es el valor del número de oro: 1,618 .
3 8 11 19 30 49 59 108 167 275 442 717 1159 1876
 1876 / 1159 = 1’618 Si cogemos por ejemplo otros dos números cualesquiera, el dos y el cinco, observamos en el dibujo que ambos segmentos distan mucho de estar en proporción áurea , no obstante podemos observar a continuación que al empezar a sumar el último más el anterior (2 + 5, 5 + 7, 7 + 12, 19 + 12, etc.), veremos que los dos últimos de la serie que tomemos se van aproximando cada vez más a la proporción áurea.
Tomamos como ejemplo el dos y el cinco. Sumamos 2 + 5 y obtenemos siete más
el anterior obtenemos 12, +7 tenemos 19, +12 obtenemos 31, +19 obtenemos 50, +31 obtenemos 81, +50 obtenemos 131, +81 obtenemos 212, de forma análoga sumando siempre los dos últimos términos obtenemos los siguientes números de la serie: 343, 555,898, 1453,2351,3804,6155, etc. Si dividimos los dos últimos de la serie tenemos como cociente el número de oro, 1,618.
En el cuadro hemos hecho una línea horizontal y hemos ido colocando de forma
vertical los segmentos con su dimensión correspondiente, guardando siempre la misma distancia entre ellos. A la derecha, en los dos últimos términos de la serie (en color verde y rojo, los correspondientes a los números 6155 y 3804), podemos observar cómo estos dos segmentos están prácticamente en exacta proporción áurea, por tanto al ir sumando siempre el segmento previo al último tenemos un nuevo segmento que es cada vez con mayor aproximación proporción áurea con el anterior. 
En la imagen se puede observar de forma gráfica como el último segmento
dibujado a la derecha en color violeta y naranja (a mas b), se obtiene sumando el anterior azul más naranja (c mas a) más el mayor del anterior en color naranja (a).
Si retrocedemos hasta el principio podemos observar en los rectángulos que siempre tomamos para obtener el último la suma de los dos anteriores mas el mayor de los anteriores. De esta forma obtenemos siempre dos medidas que cada vez se acercan más a las que corresponden a la proporción áurea. En la figura observamos un cuadrado amarillo y un rectángulo que lo inscribe. a/b = b/c esa es la proporción áurea y esta es la forma gráfica de expresarlo por proporcionalidad; podemos observar que se verifica esa igualdad ya que en el triángulo rectángulo b + c es a b como b es a c, tal y como se puede comprobar en la imagen. En la imagen a la izquierda tenemos un cuadrado con un segmento rojo FB en la parte inferior que denota la longitud del segmento áureo; la forma de expresarlo es mediante el giro de la hipotenusa del triángulo rectángulo inscrito, en la prolongación del lado base del cuadrado hasta F. En color rojo aparece el valor del número de oro. En la figura de la derecha tenemos una circunferencia de radio 1/2 y una tangente que tiene un segmento de longitud unidad al hacer la circunferencia de radio 1 obtenemos en la prolongación de la hipotenusa del triángulo rectángulo el segmento rojo que también tiene el valor del número de oro y esa es otra forma de hacer la proporción áurea gráficamente. En esta figura podemos observar un cuadrado amarillo y un rectángulo azul que tiene exactamente la misma forma aunque distinto tamaño que el rectángulo formado por ambas figuras y esa es una propiedad única del rectángulo áureo. Si al cuadrado amarillo le sumamos otro rectángulo también áureo obtenemos en la composición de los dos un rectángulo áureo, por tanto siempre podremos colocar dentro de cada rectángulo un cuadrado más otro rectángulo áureo. En la
imagen observamos que dentro de un rectángulo áureo aparecen numerosos
cuadrados que dejan siempre anexo un rectángulo áureo sobre el que colocamos
otro cuadrado y otro rectángulo áureo y así hasta el infinito y esta matriz nos
sirve para construir la espiral de Durero en el rectángulo áureo en base a que
de manera circular en espiral vamos obteniendo todos esos cuadrados que
tienden a ir hacia un punto asintótico que será el centro de esa espiral de
rectángulo áureo. En la figura podemos observar un pentágono regular y las proporciones áureas básicas que lo constituyen. Observamos el segmento azul KT (diagonal) que dividido entre el segmento K L (lado), tenemos el número de oro, mientras que si cogemos el cuadrado rojo y el fragmento de circular verde observamos también que ahí se da el número de oro ya que VS dividido entre S M es igual al número de oro y de la misma forma si cogemos el rectángulo naranja y el fragmento circular azul tenemos que PS dividido entre SW es igual al número de oro. Como podemos verificar la clave del número de oro está en el cociente entre estas relaciones del pentágono regular de ahí que ese número aparezca en numerosos poliedros como por ejemplo los regulares. En la
figura podemos observar numerosos rectángulos propuestos para comprobar si realmente es
cierto que el número de oro aparece en objetos armoniosos o más agradables
estéticamente que otros, por ello emplazamos al lector a que busque el
rectángulo más estético entre todos los que aparecen ahí advirtiendo de que
solo uno de ellos es un rectángulo áureo, mientras que los demás son rectángulos
con medidas aleatorias que no responden a la proporción áurea. Después de unos
minutos pensando cuál debe ser el más estético o el que más interesa por sus
propiedades armoniosas informamos que el rectángulo áureo es
aquel que está marcado con el número nueve. Si realmente el lector no ha dado
con él es que probablemente la cuestión armoniosa o estética de la figura se
pueda poner en cuestión, lo que no quita que muchos consideren que eso no es
cierto y lo hayan incorporado a numerosos diseños, como por ejemplo la forma
rectangular del documento nacional de identidad o de las tarjetas de crédito
que tienen la forma que corresponde a la imagen del número nueve. Si
realmente no es más estético que otro cualquiera de los que están ahí, la
cuestión armoniosa sobre la proporción áurea se podría desechar aunque
todavía nos quedaría la optimización de las plantas que utilizan el número de
oro para exponerse mejor al sol o de la adecuación botánica y biológica en
muchos seres vivos al número o incluso a nivel astronómico, como pueden ser las
espirales de las formas de las galaxias, siempre con una aproximación a la forma
del número de oro pero sin una exactitud total en sus formas. También la vemos en algunas caracolas o el crecimiento de las piñas con bastante
aproximación respecto a lo que es el número de oro y su representación gráfica, por
lo demás también a nivel geométrico tenemos que esa proporción se da matemáticamente como hemos visto en el pentágono regular y de ello se derivan muchos
polígonos que lo utilizan. En el dibujo observamos el Hombre de Vitruvio realizado por Leonardo da Vinci en el que se expresan los segmentos que establecen el cociente en proporción áurea. Como podemos observar el segmento rojo es al verde mediante ese cociente del número de oro y tal y como observamos a la izquierda lo expresamos gráficamente con los cuadrados y los fragmentos de círculo en color verde que denotan distintas relaciones en áreas dentro del cuerpo humano. Aunque hay que decir también que podríamos establecer otras muchas medidas que no se someten al número de oro o que se someten a cualquiera de las otras proporciones o relaciones que existen como por ejemplo el número pi, también si lo expresamos gráficamente lo podremos obtener en numerosos elementos del cuerpo humano sin que por ello tengamos nada fuera de lo común ya que podemos establecerlo también en cualquier otro objeto, esa proporción o cualquier otra. Por ello es necesario dejar manifiesto que si bien la proporción áurea aparece de forma clara en numerosos elementos de la naturaleza a veces por una necesidad de optimización y economía de los diseños, como el ángulo de 137º que define también la relación áurea para las circunferencias en el crecimiento armonioso de las hojas de las plantas así como otros muchos ejemplos, también son claros de una apreciación y utilidad de la proporción en distintos entornos orgánicos y biológicos además de los puramente matemáticos como las figuras basadas en el pentágono regular. -------------------------------- por ejemplo en las pirámides de Egipto, en el Partenón de Atenas, en numerosas catedrales, en gran variedad de obras pictóricas, etcétera. en el ser humano aparece de forma continua en relaciones entre huesos, la altura del ser humano está en proporción habría con la distancia de la base al ombligo. Leonardo de Pisa (Fibonacci), hizo en el siglo XIII una serie para determinar el número de parejas de conejos que se tendrían al final del año, de esta manera obtuvo la famosa serie llamada de Fibonacci: el primer mes una pareja de conejos tendría una pareja, el segundo mes tendría dos parejas el tercer mes tendría tres parejas, el cuarto mes tendría cinco parejas, el quinto mes tendría ocho parejas, el sexto mes tendría 13 parejas, etc., tenemos aquí la serie: 1,1, 2,3, 5,8, 13, cada número nuevo en la serie se obtiene sumando los dos anteriores. Después de numerosos elementos de la serie tenemos que al dividir el mayor entre el menor de dos números consecutivos de la serie, obtenemos como cociente el número de oro: 1,618033
La proporción áurea contiene muchas propiedades interesantes, aparece en pautas armónicas en los diseños naturales como plantas y pétalos de flores, los moluscos, los huracanes, remolinos y vientos, en la disposición de de semillas de frutas, de las estrellas, en espirales de la naturaleza, en cuernos de numerosos animales, etc. También se da en la disposición de la estructura del oído interno. En las conchas de moluscos observamos siempre una distribución en espiral en la que se da la proporción áurea, y esto ha servido para la construcción de numerosos detalles arquitectónicos, como por ejemplo los que corresponden al estilo jónico de las columnas de arquitecturas griegas.
El número de oro se da en los fósiles, en los vuelos de los halcones que caen hacia su presa
haciendo un espiral logarítmica expandida de forma tridimensional para tener una mejor visión de la orientación del espacio, en los cuernos del carnero, en los colmillos del elefante, en la dinámica de los agujeros negros, en los remolinos, en la disposición de los cristales en empaquetamientos estables, en empaquetamientos de estructuras microscópicas de muchos elementos, como los cristales y el hielo, en las olas de la playa se dan espirales logarítmicas, en las corrientes oceánicas, en las estrellas marinas, tanto en su disposición en forma de pentagrama como en sus protuberancias, en el crecimiento de los árboles, en las piñas de los pinos, en la estructura de las conchas, como por ejemplo el nautilo, en los pétalos de las flores, en las espirales de las galaxias, en los elementos de los girasoles, en el crecimiento de las hojas, en la espiral del ácido desoxirribonucleico, en los latidos del corazón, etc. No hay nada misterioso en la aparición de esta proporción en la naturaleza, su existencia se debe a que casi todos los elementos geométricos aquí nombrados tienen una estructura pentagonal regular, mientras que en la naturaleza se debe a que los organismos utilizan siempre una disposición que facilita su orientación hacia el sol, como es el caso del orden de las hojas de la palmera o de las escamas de la piña o de las pipas del girasol que se van distribuyendo en torno a la circunferencia mediante la proporción áurea para aprovechar mejor el espacio. Tanto los pétalos de una flor como su distribución por los tallos de las plantas siguen la proporción áurea ya que de esta manera pueden tener acceso fácil a la luz, y evitar el solapamiento de pétalos u hojas según se van distribuyendo por el tallo, siempre siguiendo las pautas de la proporción áurea. Por un lado, la geometría pentagonal determina la aparición de la proporción áurea en numerosos elementos geométricos, mientras que por otro lado los elementos naturales buscan al aprovechar la luz y el espacio ésta disposición. Existe cierta afinidad entre esta proporción y las simetrías, los elementos naturales también se someten a la búsqueda continua de simetrías, así por ejemplo una pompa de jabón buscando un estado de mínimo consumo energético se compacta hasta aparecer como una esfera. La estructura interna de los diamantes para tener una disposición más resistente se organiza mediante tetraedros de carbono, los virus se replican más fácilmente al adoptar formas con multiplicidad de simetrías ya que éstas facilitan además una mayor resistencia para su integración en la célula.
En general, en la naturaleza se da la proporción áurea para aprovechar los recursos naturales como pueden ser el sol; así el crecimiento de los pétalos o los elementos de una piña o de una flor como el girasol crecen a 137,5° respecto al último elemento, pues el arco del sector azul b y el del sector amarillo a están en proporción áurea. El arco completo de la circunferencia de 360º dividido entre 1,618 es igual a 222,5º, (el sector azul), lo que queda o sector de color amarillo se obtiene al restarle 222,5º a 360º, que es igual a los 137,5º, el ángulo de crecimiento de las hojas. Los 137,5°, como se puede ver en la imagen, evitan el solapamiento desde el nº 1 al 20 sobre la misma circunferencia, para ello se disponen los elementos en disposición de espiral o hélice cuando es una distribución tridimensional, como las ramas de un tallo. En la naturaleza el crecimiento con este ángulo permite que el pétalo u hoja que sale respecto a los anteriores pueda disponer de la luz del sol sin ser solapado o interferido por los otros, el 1º es el 0, el 2º el 1, etc. Además de la disposición angular de 137,5º, el crecimiento se hace sumando desplazamientos desde el centro hacia afuera,
En la imagen podemos observar a la izquierda un rectángulo áureo FEBD y a la
derecha un triángulo áureo NOP. Si al rectángulo áureo le quitamos un cuadrado CFEA (en color amarillo) el rectángulo que queda ABCD es idéntico en su forma al rectángulo original FEBD, se dice que son proporcionales (igual forma y distinto tamaño). Si sobre el verde quitáramos otro cuadrado el que quedaría también sería idéntico al original en su forma. Esta es una peculiaridad que se da sólo en los rectángulos áureos.
En la imagen de la derecha observamos un triángulo áureo NPO, análogamente
si se le quita un triángulo isósceles PMO, (en la imagen en color amarillo) el triángulo MNO que queda en color verde es idéntico al triángulo original NPO. De igual forma podríamos quitar al triángulo verde otro triángulo isósceles y nos quedaría al restar éste otro triángulo idéntico en su forma a los dos anteriores. -------------------------------- 
Para construir un rectángulo áureo dado el segmento medio AB de la proporción,
en el punto medio P de la base de la figura AB hacemos centro con un arco cuyo radio va desde ese punto P hasta cualquiera de los dos vértices superiores del cuadrado, por ejemplo el punto Q. Donde ese arco corta a la prolongación del lado de la base AB tenemos el nuevo punto C que determina con B el segmento BC, que está en proporción áurea con el anterior AB. Si sobre este segmento BC dibujamos un rectángulo con la misma altura que el cuadrado (en el dibujo en color amarillo) , tenemos un rectángulo áureo. Esto quiere decir que el nuevo rectángulo amarillo es proporcional al rectángulo formado por el rectángulo amarillo más el cuadrado azul, ya que el segmento mayor es al medio como el medio es al menor.
Demostración: tenemos que demostrar que el segmento mayor AC es al medio AB
como el segmento medio es al menor BC. Gráficamente lo podemos expresar mediante dos triángulos semejantes: el triángulo AMC y el triángulo ABN.
Observamos que el segmento mayor AC se transforma en el segmento medio MA o
lado del cuadrado AB, ya que MN =AB. Ahora transformamos el segmento AB en el segmento NA mediante una recta paralela BN a MC.
Se trata de demostrar que el segmento NA tiene que ser igual a BC, para que se verifique
el teorema de la proporción áurea. Haciendo una circunferencia con centro en el punto medio de la base del cuadrado O observamos que esta pasa por el punto C y por el punto K, de ello se desprende que el segmento BC es igual al segmento KA, pero éste también es igual al segmento NA, con lo que queda demostrado que AC es a MA (o AB) como MA que es a NA (o BC).
En el dibujo podemos observar un rectángulo áureo formado por un cuadrado en color
amarillo y otro rectángulo áureo en color azul. Al segmento mayor del rectángulo se le ha dado el valor 1,618, por lo que tenemos que el segmento medio vale 1 y el segmento menor vale 0,618. De esta forma tenemos que el segmento mayor es al medio, (esto es, 1,618 dividido entre uno es igual a 1,618, por lo que tenemos ya el número de oro ), como el segmento medio, esto es, uno es a el segmento menor, 0,618. De ello se desprende que uno dividido entre 0,618 es igual a 1,618, ya que existe la misma proporción entre el segmento medio y el menor que entre el mayor y el medio. Esto se puede expresar gráficamente de la siguiente forma:
En cada rectángulo áureo consideramos la proporcionalidad que existe mediante
otro rectángulo áureo menor. El rectángulo áureo mayor, determinado su segmento mayor por los puntos AC, se transforma en otro rectángulo áureo menor cuyo segmento mayor es A’B’. Pero al mismo tiempo este segmento mayor corresponde al segmento medio A’B’ del rectángulo anterior.Como podemos observar, los rectángulos áureos se van repitiendo hasta el infinito de manera que el segmento medio de cada rectángulo áureo es el mayor del siguiente, y según la progresión, el menor del primero se transforma en el medio del siguiente con lo que se hace patente la relación de proporcionalidad entre los tres segmentos: grande, medio y menor. --------------------------------
Para calcular la proporción áurea de un segmento dada la dimensión mayor DC de la
proporción, se hace un arco con centro en el extremo del segmento C y con radio AC siendo este la mitad del segmento DC. El arco corta a la vertical por C en el punto B. Unimos el punto B con el otro extremo del segmento D y hacemos centro en B con el radio BC hasta que corta al segmento DB en el punto P. Hacemos un arco con centro en el punto D y con el radio DP hasta que corta al segmento DC en el punto S, este punto define la división del segmento mayor DC entre el medio DS y el menor SC.
Si tenemos un segmento AB que queremos dividirlo según la proporción áurea, construimos una línea perpendicular por el extremo B y tomamos sobre esta la mitad de la dimensión de AB.
BC=1/2 (OB)
Construimos una circunferencia naranja de radio CB sobre la recta perpendicular, de esta manera tenemos una circunferencia tangente a la línea dada que corta a la recta OC (unión del centro de la circunferencia con el extremo del segmento dado) en el punto A.
Tomando ahora centro en el punto O y como radio la distancia OA construimos un arco (en color amarillo) hasta que corta a la línea OB en el punto G. de esta manera hemos dividido AB según la proporción áurea. Tenemos por tanto que OB/OG=OG/GB.
El fundamento de esta construcción reside en la potencia de un punto O respecto a la circunferencia naranja. Tenemos que para cualquier secante que incida sobre el centro O, lo siguiente:
OA.OA’= constante
La posición límite de cualquier secante en la circunferencia es una recta tangente que transforma los dos puntos de corte con la circunferencia en uno, de esta manera el punto homólogo de B es B’, un punto doble que se ha transformado en sí mismo.
Tenemos por tanto que OA.OA’= OB.OB’= k.
Si pasamos OA al denominador del segundo término y pasamos OB’ al denominador del primer término tenemos que OA’/OB’=OB/OA, que no es otra cosa que la proporción áurea entre OA’ OB’ y OA.
 segmento mayor de la proporción áurea en los otros dos. Primero hacemos la circunferencia amarilla con el centro en el extremo del segmento, luego la circunferencia azul tangente a la base otra vez en el extremo del segmento y por último la circunferencia naranja, tangente a la circunferencia azul y con el centro en el otro extremo del segmento.
-------------------------------- 
También podemos dividir un segmento en proporción áurea mediante proporcionalidad,
dado el segmento mayor AB.
Dado un segmento AB, se trata de determinar dónde queda el punto C.
Construimos una línea cualquiera v que pase por A. Sobre un punto M de esta recta hacemos el segmento MO paralelo al anterior AB. Calculamos el punto N por el procedimiento anterior y tenemos un rectángulo a áureo con la proporción MN/MO=MO/ON.
Alineamos el punto B con el punto N y tenemos en la intersección con la recta v
el centro de proyección P. Construimos una recta que pase por los puntos PO y donde corte su prolongación al segmento AB obtenemos el punto buscado C. 
En la figura observamos mediante un giro y traslación a la base que
la dimensión menor BC del rectángulo áureo ABC se corresponde con
la media del siguiente A'B' correspondiente a A'B'C'. De esta forma observamos
que el mayor al medio como al medio al menor se corresponde nuevamente,
el medio pasa a ser el mayor y el menor en medio, una correspondencia constatada
de forma gráfica.
Si cogemos una manzana, podemos observar que sus semillas están configuradas
según una estrella de cinco puntas, figura llamada en geometría pentagrama, y esta
figura no es otra cosa que un pentágono al que se le han añadido triángulos isósceles
a sus lados. Los vértices alternos de este pentagrama están en proporción áurea con
respecto a el lado del pentágono donde se inscriben. Las diagonales del pentágono
definen el pentagrama y en el centro del mismo otro pentágono en el que se puede
dibujar otro pentagrama invertido y así hasta el infinito. En la proporción áurea se da
una progresión continua cuyo cociente es siempre el número de oro.
--------------------------------
 Si unimos los vértices de un pentágono entre sí mediante todas sus diagonales obtenemos el pentagrama (en el dibujo en color violeta). Cada diagonal del pentagrama, o recta que une cada par de vértices opuestos del pentágono, está en proporción áurea con el lado del pentágono regular. --------------------------------
En un pentagrama el triángulo ABC se llama triángulo áureo y es aquel triángulo
isósceles cuyo lado desigual está en proporción áurea respecto a cualquiera de los otros dos lados. En la figura el triángulo de la izquierda formado por los fragmentos amarillo y naranja es un triángulo áureo. Los brazos verdes del pentagrama también son triángulos áureos.
En la figura de la derecha observamos una espiral construida a partir de este triángulo
áureo, dentro del primer triángulo se ha puesto otro menor girado y dentro de este otro y así hasta el infinito. De esta manera en cada triángulo tenemos una circunferencia correspondiente al primer arco con centro en el punto 1 y arco 1, a continuación tenemos otra circunferencia con centro en el punto 2 y arco número 2 y así sucesivamente. El enlace de todos estos arcos de circunferencia determinan la espiral. --------------------------------
En los dos dibujos del pentágono observamos que el pentágono y algunos segmentos
del mismo están en proporción áurea.
En la figura de la izquierda tenemos que AC/AB=AB/BC y AB/BD=BD/DA
En la figura de la derecha tenemos que la diagonal EG del pentagrama y el lado
del pentágono EF están en proporción áurea y EG/EF=EF/FG pero FG=HG y
GI/GH=GH/HI por lo que EG/EF=EF/HG.
--------------------------------
En la figura de la izquierda tenemos que MP/MO=MO/OP y como el segmento PO
es igual a NO tenemos que en el pentagrama MP/MO=MO/ON.
En la figura de la derecha observamos que al girar un lado del pentágono hasta
hacerlo coincidir con la diagonal JK del mismo, ambas (JK y KL) están en proporción áurea. --------------------------------
Si construimos un pentágono regular p inscrito en una circunferencia c y hacemos
la mediatriz m de uno de sus lados, cortará a la circunferencia en un punto T que unido al vértice más cercano del pentágono define el lado a del nuevo polígono regular: un decágono regular. El lado del decágono regular a está en proporción áurea con el radio de la circunferencia b en la que se inscribe:
b+a’/b= b/a’
y a’=a
--------------------------------
En la figura observamos un poliedro arquimediano obtenido por el corte de un dodecaedro
o un icosaedro. Este poliedro arquimediano se llama icosidodecaedro y observamos que en su proyección ortogonal estos segmentos del mismo están en proporción áurea. --------------------------------
Dentro de un triángulo isósceles siempre se puede hacer otro triángulo semejante
(de igual forma aunque de distinto tamaño).
En el vértice b del triángulo mayor hacemos la recta perpendicular m al lado opuesto.
Dibujamos la recta simétrica s’ de la base s respecto al eje m y ya tenemos un triángulo de igual forma aunque de distinto tamaño, ya que el ángulo c es común a ambas triángulos, y ya que acabamos de calcular el ángulo d simétrico e igual al anterior y como el triángulo mayor también tiene el ángulo e simétrico al ángulo c, tenemos que los ángulos a b son iguales.
Como podemos comprobar no es un triángulo áureo ya que el lado desigual y
uno de los lados iguales no están en proporción áurea, si lo fuera, al restar el mayor del menor quedaría un triángulo isósceles (de 2 lados iguales). El triángulo abd tendría que ser isósceles para ser áureo. --------------------------------
En la figura de la derecha podemos observar el triángulo áureo ABC, determinado
por dos diagonales y un lado del pentágono. Según la construcción que acabamos de ver, el triángulo BCD es semejanteal anterior. De igual forma el triángulo BDE también es semejante al anterior, ello es debido a que todos los segmentos de los pentagramas interiores y del pentágono están en proporción áurea.
En la figura de la izquierda comprobamos que esto es cierto, en la ilustración aparecen
segmentos que determinan proporciones áureas, por ejemplo ABC, DEF,GHE, HIJ,etc. , los determinados por los cuadrados azules y arcos ocres. -------------------------------- 
En la figura observamos una espiral construida sobre rectángulos áureos.
En cada cuadrado hacemos un arco de circunferencia cuyos extremos estén en la diagonal o vértices opuestos y cuyo centro este en el vértice de la otra diagonal. De esta manera hacemos centro primero en el punto uno, luego en el dos, luego en el tres, y así sucesivamente. Cada arco es tangente al cuadrado y al arco adyacente y ocupa el cuadrado de cada rectángulo áureo. En la siguiente página podemos observar figuras planas construidas con la sección áurea: curvas planas -------------------------------- ortogonal en sistema diédrico (consultar el sistema diédrico en el apartado de figuras) teniendo en cuenta su relación con la proporción áurea:
En la figura podemos observar la relación de la proporción áurea con dos
poliedros regulares: el icosaedro y el dodecaedro. La arista del icosaedro más la arista del dodecaedro es igual a la arista del cubo en el que se inscriben y las tres dimensiones están relacionadas mediante la proporción áurea, siendo la mayor la arista del cubo, la dimensión media la arista del icosaedro y la menor la del dodecaedro.
En la parte superior del dibujo, sobre el lado del cuadrados tenemos el rectángulo áureo
compuesto por el cuadrado verde cuyo lado es el del icosaedro y el rectángulo amarillo cuyo lado de la base es el del dodecaedro. Observamos que ambos lados suman el lado del cuadrado en el que se inscriben el dodecaedro y el icosaedro.
Podemos observar además que si tomamos el punto medio N de la base del cuadrado
verde y lo unimos con el vértice S (punto medio en la cara del cuadrado) tenemos la proyección SN de una cara del dodecaedro.
Si alineamos el centro N de la base del cuadrado AB con el vértice S obtenemos un vértice del dodecaedro T en la intersección de esta línea con la diagonal AU. Haciendo una recta vertical por el vértice T obtenemos el vértice del icosaedro, ya que ambas dimensiones son iguales, la diagonal del pentágono del dodecaedro y la arista del icosaedro. http://dodecaedro-en-icosaedro.blogspot.com.es/ http://generacion-de-poliedros.blogspot.com.es/2011/12/blog-post.html
En esta figura vemos la proyección ortogonal de un cubo en el que se inscriben los cinco
poliedros regulares.
En color verde aparece el icosaedro regular, en color rojo el dodecaedro, en su interior aparece
un cuadrado que corresponde a la vista del cubo, en el está inscrito también el tetraedro regular con sus aristas periféricas coincidentes, está en color negro también el octaedro regular.
Sobre la figura se han dibujado cuadrados de color amarillo claro con arcos de circunferencia
que acotan fragmentos naranjas, de esta manera se quiere mostrar algunos puntos importantes donde aparece el número de oro, por ejemplo entre la mitad de la arista exterior del cubo y la mitad de la arista del icosaedro, sí la mitad de la arista del cubo está en proporción áurea con la mitad de la arista del icosaedro quiere decir también que el doble también lo están, en consecuencia la arista del cubo está en proporción áurea con la arista del icosaedro y esta lo está con la arista del dodecaedro.
En la imagen de la izquierda vemos los cinco poliedros de la imagen anterior pero puestos en perspectiva axonométrica isométrica, observamos como están unos inscritos dentro de otros, por ejemplo el dodecaedro tiene algunas de sus aristas coincidentes con las aristas del icosaedro, las aristas del cubo son las diagonales de las caras pentagonales del dodecaedro, luego el tetraedro regular está inscrito dentro de el cubo y en los puntos medios de las aristas aparece el octaedro regular.
En las dos figuras del medio vemos la planta y alzado de la figura anterior.
En la figura de la derecha observamos otra perspectiva distinta de las mismas figuras
En esta imagen aparecen en la izquierda los cinco poliedros regulares inscritos unos dentro de otros, en ellos se ve la relación entre las aristas, en el centro tenemos la misma figura en perspectiva axonométrica trimétrica y a la derecha tenemos la misma figura de la izquierda pero con medidas, hemos partido de la arista del tetraedro que mide 1, 37 y hemos relacionado los tamaños de todos los demás poliedros con la del tetraedro que es realmente la diagonal de una cara del cubo central.
--------------------------------
En la figura podemos observar varios poliedros estrellados, dos de los cuatro de Képler-Poinsont. Podemos observar en sus proyecciones diédricas como los elementos están relacionados mediante múltiples proporciones áureas. Ello es debido a que éstos poliedros estrellados están íntimamente relacionados con los pentágonos regulares, de ahí sus nombres.
En la figura podemos observar las proyecciones ortogonales de los dos poliedros estrellados de la figura anterior. En estas vistas las proyecciones de algunos vértices están también en una relación áurea: GI/GH=GH/HI, JL/JK=JK/KL y AC/BC=BC/BA, DF/DE=DEEF.
--------------------------------
En la gran pirámide de Egipto de Ghiza, la relación entre sus caras y la altura de la misma es una proporción áurea. El área de cada cara equivale al área de un cuadrado cuya altura corresponde al de la pirámide, esto quiere decir que una cara triangular de la pirámide es equivalente al cuadrado que tiene como lado la altura de la pirámide. Si tomamos una cara de la pirámide y cogemos la altura de la misma y la dividimos por la mitad del lado de la base de esa cara tenemos como cociente el número de oro.
Hay muchos y diversos estudios que relacionan la proporción áurea con las pirámides de Egipto, en general todos hacen cálculos aproximados de esta relación sobre las mismas, sin que haya absoluta certeza de que hubieran utilizado este dato conociendo la proporción áurea, pudiendo ser un cálculo fruto del azar.
En la figura tenemos la gran pirámide de Egipto, sobre cualquiera de sus caras triangulares tenemos que la altura del triángulo n y la mitad del lado de la base p están en proporción áurea: n/p=1,618. (n+p/n=n/p).
Si al área de esta cara triangular le llamamos B y a la de la base de la pirámide le llamamos A tenemos que sumando las áreas de las cuatro caras triangulares y dividido este número por el área del cuadrado de la base obtenemos 1,618, el número de oro.
Si sumamos las áreas de las caras triangulares al área de la base de la pirámide y todo ello lo dividimos entre la suma de las áreas de las caras triangulares obtenemos también el número de oro, 1,618. (4B+A)/4B =1,618.
Si calculamos la altura de la pirámide desabatiendo cualquier cara triangular hasta que el vértice del triángulo corte a la altura de la pirámide veremos que la altura de la pirámide es el lado de un cuadrado cuya área C es igual al área del triángulo de cualquier cara B. En geometría se dice que el triángulo y cuadrado son equivalentes, que tienen la misma área. C=B.
En la figura podemos observar cómo construir la altura de la pirámide dada en planta. Como conocemos el lado y la altura de la cara triangular la colocamos coincidente con el plano de la planta. La proyectamos sobre el alzado y haciendo un giro con centro en O2 con radio O2-A2, donde corte al eje e de la pirámide obtenemos el vértice superior S, de esta manera obtenemos el lado del cuadrado L equivalente a la cara triangular. Como podemos observar con el abatimiento, la altura de la figura queda totalmente establecida a partir de las caras de la pirámide.
Gráficamente podemos calcular un cuadrado equivalente a un triángulo de la siguiente forma: dado el triángulo amarillo ABC, por el punto medio de su altura se hace un rectángulo GPBC con esa altura y con la misma base BC. Se hace una circunferencia del centro P con radio GP obteniendo sobre la prolongación de PC el punto J, intersección de este se segmento con la circunferencia. Construimos otra circunferencia de diámetro PJ y donde la prolongación del lado BC corta a la circunferencia (en O), lo unimos con P. El segmento PO es el lado del cuadrado (en color azul) equivalente al triángulo dado. Demostración en la página : Figuras equivalentes
-------------------------------- 
En la figura tenemos un triángulo rectángulo cuyos lados m n o están en progresión aritmética (se puede obtener uno a partir del otro mediante adicción o suma) y es conocido como triángulo egipcio, otras veces conocido como triángulo de Plutarco o de Pitágoras, sus dimensiones son 3, 4 y 5, o bien segmentos proporcionales a éstos.
Si restamos la hipotenusa n menos un cateto m obtenemos la dimensión b, si le restamos a un cateto m el otro cateto o, obtenemos la dimensión a. Podemos comprobar que el segmento a tiene la misma longitud que el segmento b y ello se expresa gráficamente al girar el segmento b hasta transformarlo en el segmento c paralelo al segmento a. Mediante una traslación se comprueba que los segmentos a y c son idénticos. Por tanto en este triángulo la hipotenusa menos un cateto es igual a un cateto menos el otro: n-m=m-o.
Una de las pirámides de Gizéh tiene este triángulo en su sección mediana, aunque este triángulo no tiene relación con el número de oro, el triángulo de la sección meridiana de la gran pirámide sí que lo tiene y es el que describimos a continuación:
Si construimos un cuadrado ABCD y a partir de su base AD obtenemos el nuevo segmento en proporción áurea DK, por el punto medio del segmento AK hacemos una semicircunferencia s, en la prolongación del segmento DC obtenemos con la intersección de esta semicircunferencia el punto J. Este triángulo que obtenemos AJK es el que corresponde al semiperfil meridiano de la gran pirámide. Si ahora a partir de la hipotenusa AK construimos otro cuadrado AKEF y su correspondiente segmento que está en proporción áurea con él, esto es, el segmento KH, comprobamos que haciendo centro en el punto K y tomando como radio JK, verificamos que el segmento KH es igual al segmento JK.
Tenemos por tanto que los segmentos AD y DK y los segmentos AK y JK están respectivamente en proporción áurea, ya que JK=KH, y que por tanto AD/DK=AK/JK.
--------------------------------
La serie de Fibonacci: Leonardo de Pisa, hoy conocido con el nombre de Fibonacci, hizo un interesante descubrimiento: construyó una serie numérica empezando por el 0, 1,1,2,… a partir de estos números empezó a sumar siempre los dos últimos: 0,1, 1,2,3, 5,8, 13,21,…(1 más 2 igual a 3, 2 +3 es igual a 5, 3 + 5 igual a 8, 5 + 8 es igual a 13, etc.) aunque no se sabe si conocía la relación que tiene esta serie con la proporción áurea, (según avanzamos, el cociente entre los 2 últimos se aproxima cada vez más al número de oro), sí se conoce que en el siglo XIII había planteado esta serie en base a la relación con la cría de los conejos.
Los números naturales son 1,2, 3,4, 5,6,… son todos números enteros. Son enteros también el cero y los números negativos, y se pueden expresar mediante el cociente entre dos enteros, salvo alguna excepción. Se pueden expresar también de forma fraccionada o con decimales, son números reales, o sea no imaginarios. Los números irracionales no se pueden expresar como razón de números enteros y su desarrollo mediante decimales es infinito, como por ejemplo raíz de dos, o raíz de tres, etcétera. La raíz de dos tiene por valor 1,41421356237…, un conjunto de números que nunca se repiten, al igual que el número de oro –phi- también es un número irracional y real. Los números reales, sean racionales o irracionales son los que corresponden a los puntos de una línea infinita.

Si hacemos rectángulos con los números de Fibonacci, y los adherimos unos a otros en una disposición vertical y en espiral como muestra la figura, el contorno de los rectángulos es un cuadrado perfecto. De igual forma al empezar a disponerlos de mayor a menor, el azul, a continuación el violeta, después el rojo y el naranja, observamos que queda un hueco cuadrado que podemos ir llenando con nuevos rectángulos hasta el infinito. Poliedros estrellados a partir de la prolongación de caras o aristas Podemos observar en el número 1 la planta y alzado del dodecaedro, al prolongar sus caras obtenemos en la intersección de esos planos que definen las caras, pirámides de base pentagonal regular que provocan el nuevo poliedro estrellado llamado pequeño dodecaedro estrellado (en color amarillo) y que observamos en el número 2. En el número 3 hemos cogido una de esas pirámides y la hemos colocado en planta y alzado mientras que en 5 vemos la axonometría isométrica del dodecaedro y en el 4 la del pequeño dodecaedro estrellado en color amarillo, cuyos vértices definen el icosaedro regular en color azul. En el número 2 hemos unido los vértices superiores de las pirámides obteniendo el icosaedro regular. Como podemos observar la arista del icosaedro regular llamada b, dividido entre la arista lateral a de una de esas pirámides reproduce como cociente el número de oro, 1,61803398, pero también obtenemos el número de oro si dividimos la arista de la pirámide a entre la arista del dodecaedro que en el dibujo llamamos c. Como podemos observar las tres aristas están relacionadas con el número de oro. En el número uno tenemos un dodecaedro que contiene a 5 tetraedros regulares, la intersección de los mismos produce el icosaedro regular, en el número 2 podemos observar el tetraedro regular en color verde que contiene a la cara naranja del icosaedro regular. Si prolongamos los lados del triángulo equilátero veremos que corta a las aristas del tetraedro dividiendo las mismas en segmentos áureos, por eso podemos ver que b partido por a es igual al número de oro. En el número 3 tenemos un icosaedro regular y en el 4 tenemos el gran dodecaedro estrellado cuyos vértices superiores de las pirámides son los puntos del dodecaedro regular. En el número 5 podemos ver los 5 tetraedros que definen en el interior el icosaedro regular como núcleo o intersección de los mismos (icosaedro regular ). En el número 1 tenemos un icosaedro regular de arista a, en el 2 hemos marcado una cara en color violeta y las tres adyacentes en amarillo, al prolongar las aristas que quedan entre los tres triángulos amarillos obtenemos las tres aristas de la pirámide que se apoya en la cara de color violeta. En el número 3 hemos colocado esas pirámides sobre el icosaedro regular obteniendo el gran dodecaedro estrellado. En el número 4 hemos obtenido otro poliedro estrellado a partir del icosaedro pero en vez de prolongar las aristas próximas a una cara hemos prolongado las caras y en la intersección de los mismos obtenemos esas pequeñas pirámides que aparecen en el primer estrellado del icosaedro, es el poliedro de color amarillo del número cuatro. En el número 5 aparece la perspectiva axonométrica isométrica del gran dodecaedro estrellado en cuyos vértices se puede observar que inciden los vértices del dodecaedro regular que inscribe al poliedro estrellado. A la arista del dodecaedro le hemos llamado b. La dimensión de esta arista b del dodecaedro es idéntica a la arista mayor m de la pirámide que se apoya en cada cara del icosaedro. Si dividimos la dimensión b entre la arista a del icosaedro azul obtenemos el número de oro. Análogamente si dividimos la arista lateral m de una de las pirámides que se apoyan en el icosaedro y la dividimos entre la arista a del icosaedro obtenemos también el número de oro. En el número 6, 7, 8 y 9, observamos de forma correspondiente el icosaedro regular en color azul, el gran dodecaedro estrellado en color magenta formado a partir del anterior con pirámides apoyadas en sus caras, en el 8, el primer estrellado del icosaedro en color amarillo, a partir de la prolongación de sus caras obtenemos sus pirámides, y en el 9 observamos el icosaedro regular azul dentro del dodecaedro regular que se obtiene como intersección de los 5 tetraedros inscritos en el dodecaedro regular. En el número 1 tenemos la pirámide que se coloca sobre cada cara del icosaedro, en el número 2 en color amarillo tenemos el icosaedro regular, en el número tres tenemos el gran icosaedro regular en color magenta, formado a partir de las pirámides del número 1 apoyadas en las caras del icosaedro del número 2. Los vértices del gran icosaedro definen un dodecaedro regular. En el número 4 tenemos el icosaedro en azul como intersección de los tetraedros regulares inscritos en el dodecaedro regular que inscribe al gran dodecaedro estrellado. Las cuatro figuras están dibujadas en planta y alzado y hemos denominado a la arista del icosaedro con la letra a, a la del dodecaedro con la letra b, ésta tiene la misma dimensión que la arista lateral de la pirámide número 1. El cociente entre b y a es el número de oro. En el número 5 observamos el gran dodecaedro estrellado en una proyección ortogonal cilíndrica. En el número 1 tenemos un icosaedro regular, poliedro que tiene las caras que son 20 triángulos equiláteros, al colocar pirámides sobre sus caras obtenemos el número 2 que es el gran dodecaedro estrellado, uno de los poliedros de Kepler, al unir los vértices superiores de cada pirámide obtenemos un dodecaedro regular que es un poliedro que tiene 12 caras que son pentágonos regulares. En el número 3 tenemos el dodecaedro regular en el que hemos inscrito un tetraedro regular, poliedro que tiene 4 caras que son triángulos equiláteros. Sobre ese poliedro regular podemos construir un icosaedro de manera que cuatro caras triangulares del icosaedro pasan por el tetraedro regular. Según la disposición del icosaedro en el número 4 tenemos la proyección correspondiente del gran icosaedro en el número 5 al que hemos incorporado el tetraedro regular interno, en el número 6 y 7 tenemos perspectivas axonométricas de ambos poliedros, el icosaedro y el estrellado. En el número 8 y 9 tenemos la misma disposición para el icosaedro y el estrellado mientras que en el 10 podemos observar lo mismo que en el número 3 pero con las caras del tetraedro coloreadas y las dos caras del icosaedro que se ven que pertenecen al tetraedro regular. Si cogemos los 5 tetraedros y los colocamos según la disposición del número 11, dentro del dodecaedro regular, obtenemos en la intersección de los 5 tetraedros el icosaedro, en el número 12 tenemos una perspectiva axonométrica de la misma figura con los 5 tetraedros y el dodecaedro externo, dejando ver como núcleo interno de intersección de los mismos el icosaedro regular centrado en la figura. En la figura número 1 observamos un octaedro regular ( poliedro que tiene 8 caras que son triángulos equiláteros), apoyado en una cara. La proyección en planta tiene por contorno un hexágono regular, en el alzado tiene un rombo y en el perfil un rectángulo. En la figura número 2 observamos el mismo poliedro en planta con contorno de cuadrado y en alzado y perfil con dos contornos en rombos, respectivamente. En la planta de esta figura número 2 observamos que una cualquiera de las aristas de la figura está dividida en los segmentos ab, esos dos segmentos están en proporción áurea eso quiere decir que si dividimos a entre b obtenemos el número de oro 1,618033. Según está proporción también podemos dividir (a + b) / a obteniendo el mismo número. Tomamos en la figura 2 sobre una cara triangular del octaedro regular y colocamos otro triángulo equilátero - aparece en color gris- de manera que los vértices de este nuevo triángulo inscrito están sobre las aristas de la cara del poliedro en proporción áurea. Al colocar sobre cada una de las caras del octaedro regular los triángulos equiláteros inscritos obtenemos un icosaedro regular ( poliedro con 20 caras que son triángulos equiláteros). En el número 3 observamos la disposición del icosaedro regular que está inscrito en el octaedro en el número 2 y cuyas caras coincidentes con el octaedro aparecen en un semitono gris rosado, (figura 1 y 2). En el número 1 también observamos el icosaedro inscrito en el octaedro, aunque con una disposición más difícil de entender que en el número 2. En el número 4 observamos la misma disposición que la planta del número 1 pero en modo alámbrico, se ha marcado en amarillo la cara del icosaedro regular y se ha puesto centrado y en proporción áurea el triángulo equilátero naranja cuyos vértices están en esa relación a áurea.
Vídeo sobre la proporción áurea: http://www.youtube.com/watch?v=d_7I-uqz_ic&feature=related
-------------------------------- |
En la figura 7 vemos un tetraedro regular inscrito en un dodecaedro regular, para inscribirlo se inscribió primero en un cubo, como sabemos un cubo es fácil de inscribir en un dodecaedro de manera que cada cara forma parte de los vértices de dos caras adyacentes.
Una vez que tenemos inscrito el tetraedro regular cogemos un eje que atraviese a todo el dodecaedro, como el de la figura 7 con la letra e, y hacemos un giro del tetraedro dejando registro de 5 tetraedros de manera que los cinco se apoyan en los vértices correspondientes del dodecaedro, de esta manera como los tetraedros regulares tienen 4 vértices, si lo multiplicamos por 5 tetraedros tenemos los 20 vértices del dodecaedro, de esta manera obtenemos la figura número 5 formada por los 5 tetraedros regulares que han girado en torno al eje, en esta figura en planta y alzado se puede observar cómo los tetraedros tienen sus vértices sobre los vértices del dodecaedro. El dodecaedro es la figura que aparece en el número 4 en planta y alzado y en el número 8 en axonometría isométrica.
En el número 3 vemos en planta y alzado los tetraedros conformando un poliedro compuesto, es lo mismo que aparece en la figura 5 pero sin que aparezca circunscrito el dodecaedro.
Si calculamos la intersección de estos 5 tetraedros regulares obtenemos el icosaedro regular, figura que aparece en el número 9 en axonometría isométrica y en el número 1 en planta y alzado, realmente esa es la escala real del icosaedro fruto de hacer la intersección de todos los tetraedros de la figura 3, poliedro compuesto de tetraedros en sistema diédrico.
En el número 2 aparece otra vez en planta y alzado el icosaedro regular pero con el eje que provocó la revolución de los tetraedros.
En el número 6 aparece una perspectiva axonométrica isométrica de los tetraedros entrelazados.
La razón de porqué la intersección de los tetraedros conforman un icosaedro es porque los 5 tetraedros se han girado igual ángulo respecto a los 360 grados de la circunferencia completa, todas las caras tienen esa misma regularidad y la única figura posible qué provoca un poliedro convexo irregular de 5 caras es el icosaedro, figura formada por antiprismas.
Poliedros del ejercicio anterior pero con estructura alámbrica
| La Proporción Áurea | Documental Redes Eduard Punset Vídeo de elementos naturales en los que se da la proporción áurea Donald en la tierra mágica de la matemática
Jamie Janover
A la izquierda
tenemos un dodecaedro regular, la diagonal de una de sus caras pentagonales y
el lado del Pentágono tienen como cociente el número de oro. Podemos ver
el dodecaedro que en la proyección ortogonal se inscribe en un cuadrado
de manera que el lado del cuadrado también está en proporción áurea con la
diagonal del Pentágono, eso quiere decir que el lado del cuadrado es a la
diagonal del Pentágono como está es al lado del Pentágono. El cociente entre
ambas es el número de oro, 1,61803398879894 Una vez que tenemos ya ubicado el Pentágono y sus relaciones
áureas, podemos coger los puntos del Pentágono y unirlos mediante la
disposición de la derecha, de esta forma obtenemos un triacontaedro rómbico,
como podemos observar es un poliedro de Catalan que tiene todas las caras
iguales, son rombos cuyo cociente entre ambas diagonales también es el número
de oro, ello es debido a que la diagonal mayor del rombo coincide con la
diagonal del Pentágono mientras que la diagonal menor coincide con el lado del
Pentágono, de esta manera podemos decir que el poliedro triacontaedro A la
izquierda tenemos un dodecaedro regular, la diagonal de una de sus caras
pentagonales y el lado del Pentágono tienen como cociente el número de
oro. Podemos ver el dodecaedro que en la proyección ortogonal se inscribe
en un cuadrado de manera que el lado del cuadrado también está en
proporción áurea con la diagonal del Pentágono, eso quiere decir que el lado
del cuadrado es a la diagonal del Pentágono como está es al lado del Pentágono.
El cociente entre ambas es el número de oro, 1,61803398879894 Una vez que tenemos ya ubicado el Pentágono y sus relaciones
áureas, podemos coger los puntos del Pentágono y unirlos mediante la
disposición de la derecha, de esta forma obtenemos un triacontaedro rómbico,
como podemos observar es un poliedro de Catalan que tiene todas las caras
iguales, son rombos cuyo cociente entre ambas diagonales también es el número
de oro, ello es debido a que la diagonal mayor del rombo coincide con la
diagonal del Pentágono mientras que la diagonal menor coincide con el lado del
Pentágono, de esta manera podemos decir que el poliedro triacontaedro r. está
circunscrito al dodecaedro, y ellos nos deja ver un nuevo método de
construcción, realmente el triacontaedro rómbico se puede obtener al añadir
pirámides a cada una de las caras pentagonales del dodecaedro regular, esas
pirámides cumplen una condición, a saber, que cada una de sus caras
triangulares tienen su plano coincidente con la cara triangular de la pirámide
adyacente, de esta manera 2 caras triangulares se convierten en una única
figura rómbica. Este mismo procedimiento vale para todos los poliedros
regulares, al tetraedro regular le podemos aumentar pirámides en sus caras con
las adyacentes coincidentes de manera que forman rombos, en este caso los
rombos son de diagonales iguales y por tanto son cuadrados, eso quiere decir
que se genera el cubo, en el caso del octaedro y cubo, podemos aumentarle
pirámides con la misma condición de que las caras adyacentes se conviertan en
rombos y obtenemos el rombododecaedro, por último tanto en el dodecaedro como
del icosaedro, al aumentarle pirámides apoyadas en sus caras y haciendo
coincidir en planos iguales a caras de pirámides adyacentes, se obtienen
rombos, todos de igual forma y tamaño, generando el triacontaedro rombico está
circunscrito al dodecaedro, y ellos nos deja ver un nuevo método de
construcción, realmente el triacontaedro rómbico se puede obtener al añadir
pirámides a cada una de las caras pentagonales del dodecaedro regular, esas
pirámides cumplen una condición, a saber, que cada una de sus caras
triangulares tienen su plano coincidente con la cara triangular de la pirámide
adyacente, de esta manera 2 caras triangulares se convierten en una única
figura rómbica. Este mismo procedimiento vale para todos los poliedros regulares, al tetraedro regular le podemos aumentar pirámides en sus caras con las adyacentes coincidentes de manera que forman rombos, en este caso los rombos son de diagonales iguales y por tanto son cuadrados, eso quiere decir que se genera el cubo, en el caso del octaedro y cubo, podemos aumentarle pirámides con la misma condición de que las caras adyacentes se conviertan en rombos y obtenemos el rombododecaedro, por último tanto en el dodecaedro como del icosaedro, al aumentarle pirámides apoyadas en sus caras y haciendo coincidir en planos iguales a caras de pirámides adyacentes, se obtienen rombos, todos de igual forma y tamaño, generando el triacontaedro rómbico. |